grids.mixins.mathops.DenseMathOpsMixin.dense_gradient#

Compute the element-wise gradient of a tensor field over a grid.

dense_gradient() is a wrapper around the two basis-dependent gradient methods (dense_contravariant_gradient() and dense_covariant_gradient()) and uses the basis input to determine the correct method to direct the call sequence to.

Parameters:

tensor_field (array-like) – The tensor field on which to compute the partial derivatives. This should be an array-like object with a compliant shape (see Notes below).
field_axes (list of str) – The coordinate axes over which the tensor_field spans. This should be a sequence of strings referring to the various coordinates of the underlying coordinate_system of the grid. For each element in field_axes, tensor_field’s i-th index should match the shape of the grid for that coordinate. (See Notes for more details).
out (array-like, optional) – An optional buffer in which to store the result. This can be used to reduce memory usage when performing computations. The shape of out must be compliant with broadcasting rules (see Notes). out may be a buffer or any other array-like object.
inverse_metric_field (array-like, optional) –
A buffer containing the inverse metric field \(g^{\mu\nu}\). inverse_metric_field can be provided to improve computation speed (by avoiding computing it in stride); however, it is not required.

The inverse metric can be derived from the coordinate system when this argument is not provided. See Notes below for details on the shape of inverse_metric_field.
basis ({'contravariant', 'covariant'}, optional) – The basis in which to compute the gradient tensor. If "covariant", then the gradient tensor will simply be the element-wise partial derivatives. If "contravariant", then the covariant solution will have its index raised using the inverse_metric_field.
output_axes (list of str, optional) –
The axes of the coordinate system over which the result should span. By default, output_axes is the same as field_axes and the output field matches the span of the input field.

This argument may be specified to expand the number of axes onto which the output field is computed. output_axes must be a superset of the field_axes.
in_chunks (bool, optional) – Whether to perform the computation in chunks. This can help reduce memory usage during the operation but will increase runtime due to increased computational load. If input buffers are all fully-loaded into memory, chunked performance will only marginally improve; however, if buffers are lazy loaded, then chunked operations will significantly improve efficiency. Defaults to False.
edge_order ({1, 2}, optional) – Order of the finite difference scheme to use when computing derivatives. See numpy.gradient() for more details on this argument. Defaults to 2.
pbar (bool, optional) – Whether to display a progress bar when in_chunks=True.
pbar_kwargs (dict, optional) – Additional keyword arguments passed to the progress bar utility. These can be any valid arguments to tqdm.tqdm().
**kwargs – Additional keyword arguments passed to dense_compute_gradient_covariant(), or dense_compute_gradient_contravariant_full().

Returns:

The computed partial derivatives. The resulting array will have a field shape matching the grid’s shape over the output_axes and an element shape matching that of field but with an additional (ndim,) sized dimension containing each of the partial derivatives for each index.

Return type:

array-like

Notes

Broadcasting and Array Shapes:

The input tensor_field must have a very precise shape to be valid for this operation. If the underlying grid (including ghost zones) has shape grid_shape = (G_1,...,G_ndim), then the spatial dimensions of the field must match exactly grid_shape[axes]. Any remaining dimensions of the field are treated as densely populated tensor indices and therefore must each have ndim elements.

Thus, if a (G1,G3,ndim,ndim,...) field is passed with field_axes = ['x','z'] (in cartesian coordinates), then the resulting output array will have shape (G1,G3,ndim,ndim,...,ndim) and out[...,1] == 0 because the field does not contain any variability over the y variable.

If output_axes is specified, then that resulting grid will be broadcast to any additional grid axes necessary.

When out is specified, it must match (exactly) the expected output buffer shape or an error will arise.

Chunking Semantics:

When in_chunks=True, chunking is enabled for this operation. In that case, the out buffer is filled iteratively by performing computations on each chunk of the grid over the specified output_axes. When the computation is performed, each chunk is extracted with an additional 1-cell halo to ensure that numpy.gradient() attains its maximal accuracy on each chunk.

Note

Chunking is (generally) only useful when out and tensor_field are array-like lazy-loaded buffers like HDF5 datasets. In those cases, the maximum memory load is only that required to load each individual chunk. If the out buffer is not specified, it is allocated fully anyways, making chunking somewhat redundant.

Inverse Metric:

In most cases, the inverse metric is computed by the coordinate system behind the scenes; however, it may be provided directly in cases where doing so is convenient. If this is done, the provided field must have a spatial portion corresponding to the grid’s shape (including ghost zones) over the output axes. Depending on the coordinate system, the provided metric may either be a rank-2 array (non-orthogonal coordinate systems) or a rank-1 array (orthogonal coordinate systems) in which each element corresponds to the diagonal element. The correct low-level callable is determined based on the coordinate system’s type.

See also

dense_element_wise_partial_derivatives: Generic form for general array-valued fields.
dense_covariant_gradient: Covariant gradient of a tensor field.
dense_contravariant_gradient: Contravariant gradient of a tensor field.
dense_compute_gradient_contravariant_full: Low-level callable version (full metric)
dense_compute_gradient_contravariant_diag: Low-level callable version (diag metric)

Examples

Contravariant Gradient of a Scalar Field

The easiest example is the derivative of a generic scalar field. In cartesian coordinates, this should behave exactly the same as the covariant gradient.

>>> from pymetric.grids.core import UniformGrid
>>> from pymetric.coordinates import CartesianCoordinateSystem2D
>>> import matplotlib.pyplot as plt
>>>
>>> # Create the coordinate system
>>> cs = CartesianCoordinateSystem2D()
>>>
>>> # Create the grid
>>> grid = UniformGrid(cs,[[-1,-1],[1,1]],[500,500],chunk_size=[50,50],ghost_zones=[[2,2],[2,2]],center='cell')
>>>
>>> # Create the field
>>> X,Y = grid.compute_domain_mesh(origin='global')
>>> Z = np.sin((X**2+Y**2))
>>>
>>> # Compute the partial derivatives.
>>> derivatives = grid.dense_gradient(Z,['x','y'],basis='contravariant')
>>>
>>> fig,axes = plt.subplots(1,3,sharey=True,sharex=True,figsize=(7,3))
>>> _ = axes[0].imshow(Z.T,origin='lower',extent=grid.gbbox.T.ravel(),vmin=-1,vmax=1,cmap='coolwarm')
>>> _ = axes[1].imshow(derivatives[...,0].T,origin='lower',extent=grid.gbbox.T.ravel(),vmin=-1,vmax=1,cmap='coolwarm')
>>> _ = axes[2].imshow(derivatives[...,1].T,origin='lower',extent=grid.gbbox.T.ravel(),vmin=-1,vmax=1,cmap='coolwarm')
>>> plt.show()

(Source code, png, hires.png, pdf)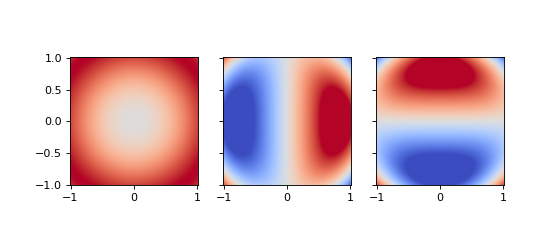

../_images/grids-mixins-mathops-DenseMathOpsMixin-dense_gradient-1.png

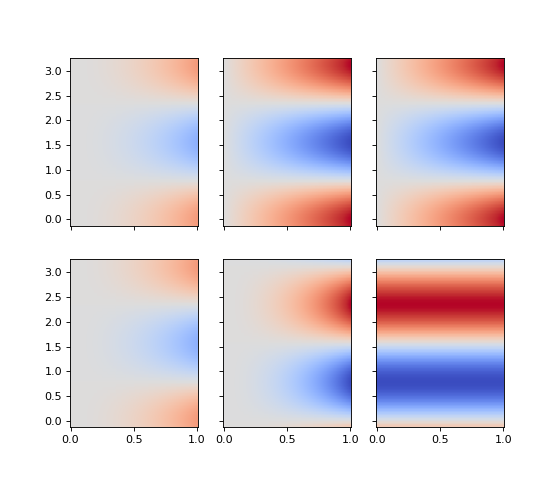
In the more interesting case, we might consider the contravariant gradient in a non-cartesian coordinate system! Let

\[\phi(r,\theta) = r^2 \cos(2\theta).\]

The covariant gradient is

\[\nabla_\mu \phi = \left[ 2r \cos(2\theta), \; -2r^2 \sin(2\theta) \right],\]

while the contravariant gradient is

\[\nabla^\mu \phi = g^{\mu\mu} \nabla_\mu \phi = \left[ 2r \cos(2\theta),\; -2\sin(2\theta) \right].\]

>>> from pymetric.grids.core import UniformGrid
>>> from pymetric.coordinates import SphericalCoordinateSystem
>>> import matplotlib.pyplot as plt
>>>
>>> # Create the coordinate system
>>> cs = SphericalCoordinateSystem()
>>>
>>> # Create the grid
>>> grid = UniformGrid(cs,[[0,1],[0,np.pi],[0,2*np.pi]],
...                   [500,50,50],
...                   chunk_size=[50,50,50],
...                   ghost_zones=[2,2,2],center='cell')
>>>
>>> # Create the field
>>> R, THETA = grid.compute_domain_mesh(origin='global',axes=['r','theta'])
>>> Z = (R**2) * np.cos(2*THETA)
>>>
>>> # Compute the partial derivatives.
>>> derivatives_cont = grid.dense_gradient(Z,['r','theta'],basis='contravariant')
>>> derivatives_co = grid.dense_gradient(Z,['r','theta'],basis='covariant')
>>>
>>> fig,axes = plt.subplots(2,3,sharey=True,sharex=True,figsize=(7,6))
>>> _ = axes[0,0].imshow(Z.T                 ,aspect='auto',origin='lower',extent=grid.gbbox.T.ravel(),vmin=-2,vmax=2,cmap='coolwarm')
>>> _ = axes[0,1].imshow(derivatives_co[...,0].T,aspect='auto',origin='lower',extent=grid.gbbox.T.ravel(),vmin=-2,vmax=2,cmap='coolwarm')
>>> _ = axes[0,2].imshow(derivatives_cont[...,0].T,aspect='auto',origin='lower',extent=grid.gbbox.T.ravel(),vmin=-2,vmax=2,cmap='coolwarm')
>>> _ = axes[1,0].imshow(Z.T                 ,aspect='auto',origin='lower',extent=grid.gbbox.T.ravel(),vmin=-2,vmax=2,cmap='coolwarm')
>>> _ = axes[1,1].imshow(derivatives_co[...,1].T,aspect='auto',origin='lower',extent=grid.gbbox.T.ravel(),vmin=-2,vmax=2,cmap='coolwarm')
>>> _ = axes[1,2].imshow(derivatives_cont[...,1].T,aspect='auto',origin='lower',extent=grid.gbbox.T.ravel(),vmin=-2,vmax=2,cmap='coolwarm')
>>> plt.show()

(Source code, png, hires.png, pdf)

../_images/grids-mixins-mathops-DenseMathOpsMixin-dense_gradient-2.png

grids.mixins.mathops.DenseMathOpsMixin.dense_gradient#

This Page