SphericalCoordinateSystem

class coordinates.coordinate_systems.SphericalCoordinateSystem(**kwargs)

3 Dimensional Spherical coordinate system.

The spherical coordinate system is defined by the coordinates \((r, \theta, \phi)\), where \(r\) is the radial distance, \(\theta\) is the polar angle, and \(\phi\) is the azimuthal angle. This system is ideal for spherical symmetries, such as in gravitational and electrostatic fields.

Conversion between spherical and Cartesian coordinates follows these standard transformations:

\[\begin{split}\begin{aligned} \text{To Cartesian:} & \quad x = r \sin(\theta) \cos(\phi), \\ & \quad y = r \sin(\theta) \sin(\phi), \\ & \quad z = r \cos(\theta) \\ \text{From Cartesian:} & \quad r = \sqrt{x^2 + y^2 + z^2}, \\ & \quad \theta = \arccos\left(\frac{z}{r}\right), \\ & \quad \phi = \arctan2(y, x) \end{aligned}\end{split}\]

Notes

The Lame coefficients for each axis in the spherical coordinate system are provided in the table below, reflecting the scaling factors due to curvature in radial and angular directions.

Axis	Lame Coefficient
\(r\)	\(1\)
\(\theta\)	\(r\)
\(\phi\)	\(r \sin(\theta)\)

Examples

The Spherical coordinate system is visualized with circles (constant r) and lines radiating from the origin (constant theta) on a 2D slice.

>>> import matplotlib.pyplot as plt
>>> from pymetric.coordinates.coordinate_systems import SphericalCoordinateSystem

Initialize the coordinate system:

>>> coordinate_system = SphericalCoordinateSystem()

Define radial and angular ranges:

>>> r_vals = np.linspace(0, 1, 6)  # Radial distances
>>> theta_vals = np.linspace(0, np.pi, 12)  # Angular values
>>> phi = 0  # Fix the azimuthal angle

Plot circles (constant r):

>>> for r in r_vals:
...     theta = np.linspace(0, np.pi, 200)
...     coords = [r * np.ones_like(theta), theta, np.full_like(theta, phi)]
...     cartesian = coordinate_system._convert_native_to_cartesian(*coords)
...     _ = plt.plot(cartesian[0],cartesian[2], 'k-', lw=0.5)

Plot radial lines (constant theta):

>>> for theta in theta_vals:
...     r = np.linspace(0, 1, 200)
...     coords = [r, theta * np.ones_like(r), np.full_like(r, phi)]
...     cartesian = coordinate_system._convert_native_to_cartesian(*coords)
...     _ = plt.plot(cartesian[0],cartesian[2], 'k-', lw=0.5)

>>> _ = plt.title('Spherical Coordinate System (Slice)')
>>> _ = plt.xlabel('x')
>>> _ = plt.ylabel('z')
>>> _ = plt.axis('equal')
>>> plt.show()

(Source code, png, hires.png, pdf)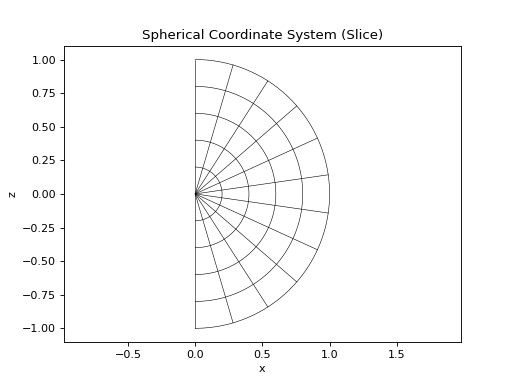

Methods

__init__(**kwargs)	Initialize a coordinate system instance with specific parameter values.
adjust_dense_tensor_signature(tensor_field, ...)	Raise and/or lower multiple tensor slots in one call.
axes_complement(axes)	Return all axes in the coordinate system that are not present in axes.
build_axes_mask(axes)	Construct a boolean mask array indicating which axes are in axes.
compute_expression(expression, coordinates)	Evaluate a named symbolic expression over mixed coordinate inputs.
compute_expression_from_coordinates(...[, ...])	Evaluate a named expression over 1D coordinate arrays with optional fixed axes.
compute_function_from_coordinates(func, ...)	Evaluate a function over 1D coordinate arrays with optional fixed axes.
convert_axes_to_indices(axes)	Convert axis name(s) to their corresponding index or indices.
convert_indices_to_axes(axes_indices)	Convert axis index or indices to their corresponding axis name(s).
convert_to(target_system, *native_coords)	Convert coordinates from this system to another coordinate system via Cartesian intermediate.
coordinate_meshgrid(*coordinate_arrays[, ...])	Construct a coordinate-aligned meshgrid from 1D coordinate arrays.
create_coordinate_list(coordinate_arrays, /)	Assemble a list of coordinate components (arrays or scalars) in canonical axis order.
from_cartesian(*coords)	Convert Cartesian coordinates to native coordinates in this system.
from_hdf5(filename[, group_name, registry])	Save this coordinate system to HDF5.
get_axes_from_mask(mask)	Convert a boolean axis mask into a list of axis names.
get_axes_latex(axes)	Return the LaTeX representation(s) of one or more axis names.
get_axes_order(src_axes, dst_axes)	Compute the reordering indices that will reorder src_axes into the order of dst_axes.
get_axes_permutation(src_axes, dst_axes)	Compute the permutation needed to reorder src_axes into dst_axes.
get_axes_units(unit_system)	Resolve the physical units for each axis in a given unit system.
get_canonical_axes_order(src_axes)	Compute the permutation indices to reorder src_axes into sorted alphabetical order.
get_canonical_axes_permutation(axes)	Compute the permutation needed to reorder axes into the canonical order defined by the coordinate system.
get_class_expression(expression_name)	Retrieve a derived expression for this coordinate system by name.
get_conversion_transform(other)	Construct a coordinate transformation function that maps native coordinates from this coordinate system to the target coordinate system.
get_expression(expression_name)	Retrieve an instance-specific symbolic expression.
get_free_fixed([axes, fixed_axes])	Split a list of coordinate axes into fixed and free components.
get_indices_from_mask(mask)	Convert a boolean mask of length ndim back to numeric indices.
get_mask_from_axes(axes)	Return a boolean mask of shape (ndim,) with True on the positions corresponding to axes.
get_mask_from_indices(indices)	Boolean mask that is True at the supplied numeric indices.
get_numeric_expression(expression_name)	Retrieve a numerically evaluable version of a coordinate system expression given the expression name.
has_class_expression(expression_name)	Check if the coordinate system has a specific expression registered to it.
has_expression(expression_name)	Check if a symbolic expression is registered at the instance level.
in_axes_order(iterable, src_axes, dst_axes)	Reorder a sequence of values from src_axes order to dst_axes order.
in_canonical_order(iterable, src_axes)	Reorder a sequence of values from src_axes order to canonical axis order.
insert_fixed_axes(iterable, src_axes[, ...])	Insert fixed axis values into an iterable of values according to canonical axis order.
is_axes_subset(axes_a, axes_b)	Check if axes_a is a subset of axes_b.
is_axes_superset(axes_a, axes_b)	Check if axes_a is a superset of axes_b.
is_axis(axis)	Check whether the given axis name(s) exist in this coordinate system.
lambdify_expression(expression)	Convert a symbolic expression into a callable function.
list_class_expressions()	List the available coordinate system expressions.
list_expressions()	List the available instance-level expressions.
lower_index_dense(tensor_field, index, rank, ...)	Lower a single tensor index using \(g_{ab}\).
order_axes(src_axes, dst_axes)	Reorder src_axes into the order defined by dst_axes.
order_axes_canonical(src_axes)	Reorder a list of axis names into the canonical order of this coordinate system.
pprint()	Print a detailed description of the coordinate system, including its axes, parameters, and expressions.
raise_index_dense(tensor_field, index, rank, ...)	Raise a single tensor index using \(g^{ab}\).
requires_expression(value, expression, ...)	Return value if not None; otherwise evaluate compute_expression.
requires_expression_from_coordinates(value, ...)	Return value if not None; otherwise evaluate compute_expression_from_coordinates.
resolve_axes([axes, require_subset, ...])	Normalize and validate a user-supplied list of axis names.
set_expression(expression_name, expression)	Set a symbolic expression at the instance level.
substitute_expression(expression)	Replace symbolic parameters with numerical values in an expression.
to_cartesian(*coords)	Convert native coordinates to Cartesian coordinates.
to_hdf5(filename[, group_name, overwrite])	Save this coordinate system to HDF5.

Attributes

axes	The axes names present in this coordinate system.
axes_dimensions	Return the symbolic physical dimensions associated with each axis.
axes_symbols	The symbols representing each of the coordinate axes in this coordinate system.
inverse_metric_tensor	Returns the callable function for the inverse metric tensor of the coordinate system.
inverse_metric_tensor_symbol	The symbolic inverse metric tensor for this coordinate system instance.
metric_tensor	Returns the callable function for the metric tensor of the coordinate system.
metric_tensor_symbol	The symbolic array representing the metric tensor.
ndim	The number of dimensions spanned by this coordinate system.
parameter_symbols	Get the symbolic representations of the coordinate system parameters.
parameters	The parameters of this coordinate system.