grids.mixins.mathops.DenseMathOpsMixin.dense_element_wise_partial_derivatives#

Compute the element-wise partial derivatives of an array-valued field over the grid.

This method computes the partial derivatives along each of the ndim axes of the grid for each element of an array-valued input field. Thus,

\[T_{ijk\ldots} \to T_{ijk\ldots;\mu} = \partial_\mu T_{ijk\ldots}.\]

Hint

Under the hood, this method wraps dense_element_wise_partial_derivatives().

Parameters:

field (array-like) – The array-valued field on which to compute the partial derivatives. This should be an array-like object with a compliant shape (see Notes below).
field_axes (list of str) – The coordinate axes over which the field spans. This should be a sequence of strings referring to the various coordinates of the underlying coordinate_system of the grid. For each element in field_axes, field’s i-th index should match the shape of the grid for that coordinate. (See Notes for more details).
out (array-like, optional) – An optional buffer in which to store the result. This can be used to reduce memory usage when performing computations. The shape of out must be compliant with broadcasting rules (see Notes). out may be a buffer or any other array-like object.
output_axes (list of str, optional) –
The axes of the coordinate system over which the result should span. By default, output_axes is the same as field_axes and the output field matches the span of the input field.

This argument may be specified to expand the number of axes onto which the output field is computed. output_axes must be a superset of the field_axes.
in_chunks (bool, optional) – Whether to perform the computation in chunks. This can help reduce memory usage during the operation but will increase runtime due to increased computational load. If input buffers are all fully-loaded into memory, chunked performance will only marginally improve; however, if buffers are lazy loaded, then chunked operations will significantly improve efficiency. Defaults to False.
edge_order ({1, 2}, optional) – Order of the finite difference scheme to use when computing derivatives. See numpy.gradient() for more details on this argument. Defaults to 2.
pbar (bool, optional) – Whether to display a progress bar when in_chunks=True.
pbar_kwargs (dict, optional) – Additional keyword arguments passed to the progress bar utility. These can be any valid arguments to tqdm.tqdm().
**kwargs – Additional keyword arguments passed to dense_element_wise_partial_derivatives().

Returns:

The computed partial derivatives. he returned array has shape: (...grid_shape over `output_axes`, ...element_shape of `field`, ndim) The final axis contains the partial derivatives with respect to each coordinate axis in the grid’s coordinate system.

Return type:

array-like

Notes

Broadcasting and Array Shapes:

The input field must have a very precise shape to be valid for this operation. If the underlying grid (including ghost zones) has shape grid_shape = (G_1,...,G_ndim), then the spatial dimensions of the field must match exactly grid_shape[axes]. Any remaining dimensions of the field are treated as elements of the field.

Thus, if a (G1,G3,F1,F2,F3) field is passed with field_axes = ['x','z'] (in cartesian coordinates), then the resulting output array will have shape (G1,G3,F1,F2,F3,3) and out[...,1] == 0 because the field does not contain any variability over the y variable.

If output_axes is specified, then that resulting grid will be broadcast to any additional grid axes necessary.

When out is specified, it must match (exactly) the expected output buffer shape or an error will arise.

Chunking Semantics:

When in_chunks=True, chunking is enabled for this operation. In that case, the out buffer is filled iteratively by performing computations on each chunk of the grid over the specified output_axes. When the computation is performed, each chunk is extracted with an additional 1-cell halo to ensure that numpy.gradient() attains its maximal accuracy on each chunk.

Note

Chunking is (generally) only useful when out and field are array-like lazy-loaded buffers like HDF5 datasets. In those cases, the maximum memory load is only that required to load each individual chunk. If the out buffer is not specified, it is allocated fully anyways, making chunking somewhat redundant.

See also

dense_covariant_gradient: Covariant gradient of a tensor field.
dense_contravariant_gradient: Contravariant gradient of a tensor field.
dense_element_wise_partial_derivatives: Low-level callable version.

Examples

Derivatives of a scalar field:

The easiest example is the derivative of a generic scalar field.

>>> from pymetric.grids.core import UniformGrid
>>> from pymetric.coordinates import CartesianCoordinateSystem2D
>>> import matplotlib.pyplot as plt
>>>
>>> # Create the coordinate system
>>> cs = CartesianCoordinateSystem2D()
>>>
>>> # Create the grid
>>> grid = UniformGrid(cs,[[-1,-1],[1,1]],[500,500],chunk_size=[50,50],ghost_zones=[[2,2],[2,2]],center='cell')
>>>
>>> # Create the field
>>> X,Y = grid.compute_domain_mesh(origin='global')
>>> Z = np.sin((X**2+Y**2))
>>>
>>> # Compute the partial derivatives.
>>> derivatives = grid.dense_element_wise_partial_derivatives(Z,['x','y'])
>>>
>>> fig,axes = plt.subplots(1,3,sharey=True,sharex=True,figsize=(7,3))
>>> _ = axes[0].imshow(Z.T,origin='lower',extent=grid.gbbox.T.ravel(),vmin=-1,vmax=1,cmap='coolwarm')
>>> _ = axes[1].imshow(derivatives[...,0].T,origin='lower',extent=grid.gbbox.T.ravel(),vmin=-1,vmax=1,cmap='coolwarm')
>>> _ = axes[2].imshow(derivatives[...,1].T,origin='lower',extent=grid.gbbox.T.ravel(),vmin=-1,vmax=1,cmap='coolwarm')
>>> plt.show()

(Source code, png, hires.png, pdf)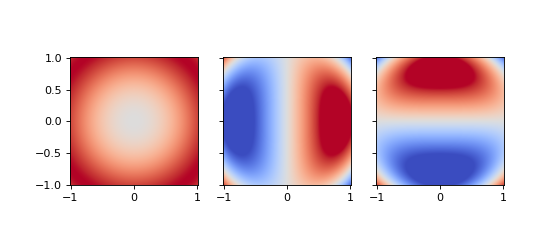

../_images/grids-mixins-mathops-DenseMathOpsMixin-dense_element_wise_partial_derivatives-1.png

Derivatives of an array field:

Similarly, this can be applied to array fields of any sort.

>>> from pymetric.grids.core import UniformGrid
>>> from pymetric.coordinates import CartesianCoordinateSystem2D
>>> import matplotlib.pyplot as plt
>>>
>>> # Create the coordinate system
>>> cs = CartesianCoordinateSystem2D()
>>>
>>> # Create the grid
>>> grid = UniformGrid(cs,[[-1,-1],[1,1]],[500,500],chunk_size=[50,50],ghost_zones=[[2,2],[2,2]],center='cell')
>>>
>>> # Create the field
>>> X,Y = grid.compute_domain_mesh(origin='global')
>>> Z = np.stack([np.sin((X**2+Y**2)),np.sin(5*(X**2+Y**2))],axis=-1) # (504,504,2)
>>>
>>> # Compute the partial derivatives.
>>> derivatives = grid.dense_element_wise_partial_derivatives(Z,['x','y'])
>>>
>>> fig,axes = plt.subplots(2,3,sharey=True,sharex=True,figsize=(7,6))
>>> _ = axes[0,0].imshow(Z[...,0].T,origin='lower',extent=grid.gbbox.T.ravel(),vmin=-1,vmax=1,cmap='coolwarm')
>>> _ = axes[0,1].imshow(derivatives[...,0,0].T,origin='lower',extent=grid.gbbox.T.ravel(),vmin=-1,vmax=1,cmap='coolwarm')
>>> _ = axes[0,2].imshow(derivatives[...,0,1].T,origin='lower',extent=grid.gbbox.T.ravel(),vmin=-1,vmax=1,cmap='coolwarm')
>>> _ = axes[1,0].imshow(Z[...,1].T,origin='lower',extent=grid.gbbox.T.ravel(),vmin=-1,vmax=1,cmap='coolwarm')
>>> _ = axes[1,1].imshow(derivatives[...,1,0].T,origin='lower',extent=grid.gbbox.T.ravel(),vmin=-5,vmax=5,cmap='coolwarm')
>>> _ = axes[1,2].imshow(derivatives[...,1,1].T,origin='lower',extent=grid.gbbox.T.ravel(),vmin=-5,vmax=5,cmap='coolwarm')
>>> plt.show()

(Source code, png, hires.png, pdf)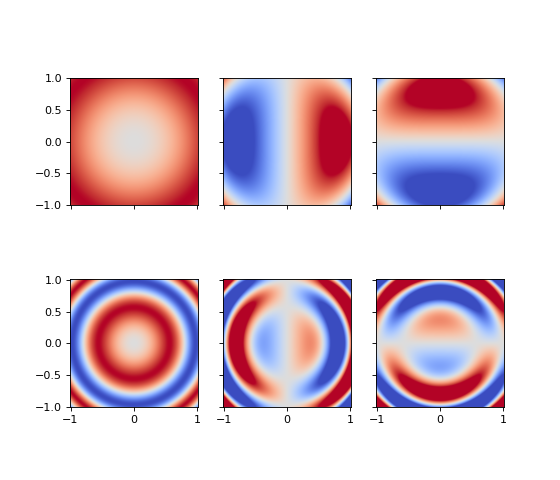

../_images/grids-mixins-mathops-DenseMathOpsMixin-dense_element_wise_partial_derivatives-2.png

Expanding to output axes:

In some cases, you might have a field \(T_{ijk\ldots}(x,y)\) and you may need \(\partial_\mu T_{ijk\ldots}(x,y,z)\). This can be achieved by declaring the output_axes argument.

>>> from pymetric.coordinates import CartesianCoordinateSystem3D
>>>
>>> # Create the coordinate system
>>> cs = CartesianCoordinateSystem3D()
>>>
>>> # Create the grid
>>> grid = UniformGrid(cs,[[-1,-1,-1],[1,1,1]],[50,50,50],chunk_size=[5,5,5],ghost_zones=[2,2,2],center='cell')
>>>
>>> # Create the field
>>> X,Y = grid.compute_domain_mesh(origin='global',axes=['x','y'])
>>> Z = np.stack([np.sin((X**2+Y**2)),np.sin(5*(X**2+Y**2))],axis=-1) # (54,54,2)
>>>
>>> # Compute the partial derivatives.
>>> derivatives = grid.dense_element_wise_partial_derivatives(Z,['x','y'],output_axes=['x','y','z'])
>>> derivatives.shape
(54, 54, 54, 2, 3)

grids.mixins.mathops.DenseMathOpsMixin.dense_element_wise_partial_derivatives#

This Page