PlummerDensityProfile#

class profiles.density.PlummerDensityProfile(**kwargs)[source]#

Plummer Density Profile.

The Plummer profile is commonly used to model the density distribution of star clusters or spherical galaxies. It features a central core and a steep falloff at larger radii [1].

\[\rho(r) = \frac{3M}{4\pi r_s^3} \left(1 + \left(\frac{r}{r_s}\right)^2\right)^{-5/2}\]

where:

\(M\) is the total mass.
\(r_s\) is the scale radius.

Expressions

Expressions for `PlummerDensityProfile`#
Name	Symbol	Notes
`spherical_mass`	\(M(r) = M\,\bigl(\tfrac{r}{\sqrt{r^2 + r_s^2}}\bigr)^{3}\)	None
`spherical_potential`	\(\Phi(r) = -\,\frac{M}{\sqrt{r^2 + r_s^2}}\)	Multiplicative constants (e.g. G) can be included externally
`surface_density`	\(\Sigma(R) = \frac{M\,r_s^2}{\pi\,\bigl(r_s^2 + R^2\bigr)^{2}}\)	On-demand expression for projected (2D) density
`ellipsoidal_psi`	\(\psi(r) = 2\int_{0}^{r}\!\xi\,\rho(\xi)\,d\xi\)	Inherited from base

References

Example

>>> import matplotlib.pyplot as plt
>>> from pisces.profiles.density import (
...     PlummerDensityProfile,
... )

>>> r = np.linspace(0.1, 10, 100)
>>> profile = PlummerDensityProfile(M=1.0, r_s=1.0)
>>> rho = profile(r)

>>> _ = plt.loglog(
...     r, rho, "k-", label="Plummer Profile"
... )
>>> _ = plt.xlabel("Radius (r)")
>>> _ = plt.ylabel("Density (rho)")
>>> _ = plt.legend()
>>> plt.show()

(Source code, png, hires.png, pdf)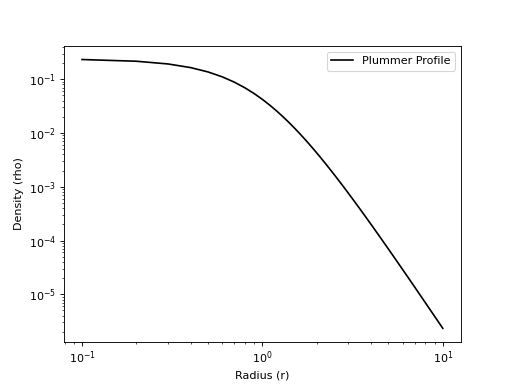

../_images/profiles-density-PlummerDensityProfile-1.png

Methods

`__init__`(**kwargs)	Initialize a profile instance with specific parameter values.
`compute_circular_velocity`(r[, units, G])	Compute the circular velocity at radius \(r\).
`compute_cosmological_overdensity_profile`(z, R)	Compute the spherical overdensity profile relative to the critical density at redshift \(z\).
`compute_cosmological_overdensity_radius`(z, ...)	Find the radius enclosing a target overdensity relative to the critical density at redshift \(z\).
`compute_deflection_angle`(R[, mode, units, ...])	Compute the gravitational lensing deflection angle at projected radius \(R\).
`compute_einstein_radius`(z_lens, z_source[, ...])	Compute the Einstein ring angular radius \(\\theta_E\) for a perfectly aligned source-lens system.
`compute_enclosed_mass`(r[, units])	Numerically compute the enclosed mass \(M(r)\) within radius \(r\).
`compute_escape_velocity`(r[, units, G])	Compute the escape velocity at radius \(r\).
`compute_fractional_mass_radius`(rmin, rmax[, ...])	Find the radius enclosing a given fraction of the total mass.
`compute_gravitational_field`(r[, units, G])	Numerically compute the gravitational field \(g(r)\) at radius \(r\).
`compute_gravitational_potential`(r[, units, G])	Numerically compute the gravitational potential \(\Phi(r)\).
`compute_lensing_convergence`(R, z_lens, z_source)	Compute the lensing convergence \(\kappa(R)\) at projected radius \(R\).
`compute_surface_density`(R[, units])	Numerically compute the projected surface density at radius R from the origin.
`compute_total_mass`([units])	Numerically compute the total mass of the profile by integrating to infinity.
`from_dict`(data)	Reconstruct a profile instance from a dictionary.
`from_hdf5`(h5obj[, name])	Reconstruct a profile from HDF5 attributes.
`from_json`(filepath)	Reconstruct a profile from a JSON file.
`from_yaml`(filepath)	Reconstruct a profile from a YAML file.
`get_derived_profile`(profile_name, **kwargs)	Access and instantiate a derived profile by name.
`get_expression_latex`([substitute])	Return the LaTeX representation of the profile's symbolic expression.
`get_output_units`(*argu)	Determine the output units of the operation given some set of input units.
`get_parameters_latex`()	Return a LaTeX table of the profile parameters.
`lambdify_expression`(expression)	Convert a symbolic expression into a callable function.
`list_derived_profiles`()	List all available derived profiles for this instance.
`substitute_expression`(expression)	Replace symbolic parameters with numerical values in an expression.
`to_dict`()	Serialize this profile to a minimal dictionary representation.
`to_hdf5`(h5obj[, name])	Store profile metadata into an HDF5 object as attributes.
`to_json`(filepath, **kwargs)	Serialize the profile to a JSON file.
`to_yaml`(filepath, **kwargs)	Serialize the profile to a YAML file.

Attributes

`derived_profile_classes`	Get the available derived profile classes for this instance.
`parameter_symbols`	Get the symbolic representations of the coordinate system parameters.
`parameters`	The parameters of this coordinate system.
`variable_symbols`	The symbols representing each of the coordinate axes in this coordinate system.
`variables`	The axes names present in this coordinate system.

Name	Symbol	Description
`M`	\(M\)	Total mass
`r_s`	\(r_s\)	Scale radius

PlummerDensityProfile#

This Page